En cirkel
En cirkel er en geometrisk figur, hvor alle punkter har en konstant afstand, kaldet radius, fra et punkt, som er cirklens centrum.
En trekant
En trekant er en geometrisk figur med tre hjørner og tre sider. De findes i mange forskellige former, såsom ret-, stump- og spidsvinklede trekanter for ikke at tale om de ligebenede trekanter m.v. I de små klasser er det vigtigste dog, at børnene ved og har set de mange former for trekanter og ikke, hvad de kaldes i fagsprog
Firkanter
I indskolingen skelner vi mellem to typer firkanter - kvadrater og rektangler.Et kvadrat
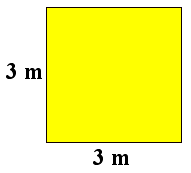
Et kvadrat er en firkant, hvor alle 4 sider er lige lange, og hvor alle vinkler er præcis 90 grader. (Såkaldte rette vinkler)
Et rektangel er en firkant, hvor de modstående sider er lige lange, og hvor alle vinkler er 90 grader.
Omkreds og areal:
I nedenstående video får du en gennemgang af, hvordan man finder areal og omkreds af et rektangel og et kvadrat.Diagonaler
En diagonal er et linjestykke, der forbinder to hjørner i en geometrisk figur. Dette gælder dog ikke figurens medtagne sider. Klik på nedenstående video og se 5 eksempler på, hvad diagonaler er, og hvordan de laves.
Symmetriakse
(Også kaldet for en spejlingsakse)En symmetriakse er en linje, som deler i figur i to dele, hvoraf hver del er den modsatte dels spejlbillede.
Spejling
En spejling inden for matematikken kan egentlig tænkes, som når du selv ser dig i spejlet! Det er, som om der står en kopi "på den anden side".Når man spejler en figur, finder man afstanden fra et punkt og vinkelret ind på spejlingsaksen (symmetriaksen). På den anden side af symmetriaksen går man lige så langt ud på den modsatte side og afsætter et nyt punkt. Det bliver så til den nye figur som vist på følgende video.
Flytning/parallelforskydning
Ligesom man kan spejle en figur, kan man også flytte den. Man parallelforskyder den ved at forskyde alle punkter lige langt i samme retning. Se billedet.Ligedannede figurer
To figurer er ligedannede, hvis den ene figur er en forstørrelse eller en formindskelse af den anden figur, eller hvis figurerne er kongruente.
